mechanisch-dynamisch
Schwingungen kehren periodisch wieder. Bekannt sind im Allgemeinen viele dieser Erscheinungen, wie Fahrzeugschwingungen, von Motoren hervorgerufene Vibrationen, Bewegungen von Schiffen im Seegang usw.
Stöße beschränken sich auf hin und wieder auftretende Ereignisse, wie sie bei Schlag, Fall oder Umkippen zu beobachten sind. In den Worten Anstoßen, Abstoßen oder Rangierstoß ist Wesentliches bereits deutlich gemacht.
Die absolute Größe beider Belastungsarten wird mit ihren Amplituden gemessen. Bei den Schwingungen ist die zweite wichtige Größe die Frequenz, also die Anzahl der periodisch wiederkehrenden Schwingungen innerhalb eines bestimmten Zeitraums [1/s]. Bei Stößen ist neben der Amplitude die Impulsdauer und die Häufigkeit entscheidend.
Mechanisch-dynamische Versandbeanspruchungen werden demnach primär durch Beschleunigungen infolge von Richtungs- oder Geschwindigkeitsänderungen bewirkt. Die Beschleunigungswerte sind besonders groß, wenn diese Änderungen sehr schnell erfolgen. Die Formeln verdeutlichen den Zusammenhang:
da
ist, folgt, dass die geradlinige Beschleunigung sich auch aus folgender Formel errechnen lässt:
Beschleunigt ein Auto in 12 Sekunden von 0 auf 108 km/h, hat es seine Geschwindigkeit in jeder Sekunde um 9 km/h bzw. 2,5 m/s geändert.
Die Beschleunigung a beträgt demnach 9 (km/h)/s oder anders ausgedrückt
2,5 m/(s · s) bzw. 2,5 m/s². Benötigt ein Lastkraftwagen aus einer Geschwindigkeit von 90 km/h heraus fünf Sekunden, um bis zum Stillstand abzubremsen, so verzögert er mit 18 km/h pro Sekunde bzw. 5 m/s pro Sekunde. Das ist exakt die in der Straßenverkehrszulassungsordnung und den Unfallverhütungsvorschriften geforderte Bremsverzögerung von 5 m/s².
Ein Schiff, das beim Einsetzen in grobe See einen Geschwindigkeitsverlust von 21 Knoten auf 9,3 kn innerhalb von 2 Sekunden erfährt, wird mit
-11,7 kn/2 s = -5,85 kn/s = -10,834 (km/h)/s = -3 m/s² negativ beschleunigt und somit verzögert.
Beschleunigungen infolge von Richtungsänderungen lassen sich nach der folgenden Formel berechnen:
Durchfährt ein Straßenfahrzeug eine enge Kurve von 20 m Kurvenradius mit einer Geschwindigkeit von 36 km/h, entsprechend 10 m/s, so erfährt es eine Kurvenbeschleunigung von 5 m/s².
Beim Durchfahren von Schlaglöchern werden gleichfalls Radialbeschleunigungen wirksam, denn es kommt zu einer Richtungsänderung aus der Horizontalen in die Vertikale und zurück. Bei schlecht gedämpften Fahrzeugen bewirkt dies erhebliche Beschleunigungen, da die Kurvenradien sehr klein und die Geschwindigkeiten, mit denen sie überfahren werden, relativ groß sind. Nur die Federung und andere konstruktive Einflussgrößen schützen in diesem Fall das Fahrzeug und die Ladung vor drastischen Beschädigungen. Bei ungefederten Rolltrailern können Unebenheiten des Terminalgeländes zu hohen Beschleunigungen mit Folgeschäden an der Ladung führen. Schon häufiger sind bei derartigen innerbetrieblichen Transportvorgängen Versandstücke von den Trailern gefallen.
 |
Durch die Schwerkraft, auch Gravitation genannt, erfährt jeder Körper auf der Erde eine nach unten gerichtete Beschleunigung, die als Erdbeschleunigung bezeichnet wird. Das Maß dieser Beschleunigung ist konstant. Die Größe der Erdbeschleunigung beträgt gerundet 9,81 m/s² und wird als 1 g bezeichnet. Für Rechnungen nach Faustregel kann 1 g auch mit 10 m/s² angenommen werden. Zur besseren Vorstellung des Beschleunigungswertes von 1 g sei angenommen, dass ein Straßenfahrzeug in 3 Sekunden von 0 km/h auf knapp 106 km/h beschleunigt. Die Rechnung sieht so aus: |
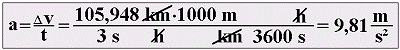
Ist eine Beschleunigung der Größe nach bekannt, kann ihre auf eine Masse wirkende Kraft nach dem Newton'schen Gesetz ermittelt werden:
GGebräuchliche Formelschreibweisen sind:
Kraft und Gewicht sind physikalisch auf der Erde identisch. Ein Körper von 100 kg Masse übt infolge der Erdbeschleunigung eine Kraft von F = 100 kg · 9,81 m/s² = 981 N auf seine Unterlage aus. In anderen Maßeinheiten sind das 98,1 daN (Dekanewton) oder 0,981 kN (Kilonewton).
Unter der Gewichtskraft ist demnach die Kraft zu verstehen, mit der ein Körper von der Erde angezogen wird. Die Wirkrichtung dieser Kraft zeigt immer senkrecht nach unten. Die verwendete Formel ist wie oben, statt der allgemeinen Abkürzung F für Force wird allerdings G gewählt.
In einigen Publikationen - so auch den VDI-Richtlinien - wird von der Normalkraft gesprochen, das Formelzeichen F mit dem Index N versehen, also FN = Normalkraft.
Kraft und Beschleunigung sind gerichtete Größen, so genannte Vektoren. Die Erdbeschleunigung g zeigt jedoch stets in die gleiche Richtung wie das Gewicht.
 |
Ein Motorradfahrer, der mit 72 km/h eine Kurve mit einem Radius von 50 m durchfährt, erfährt dabei eine Radialbeschleunigung von 8 m/s² (ar= v²/t = 20 m/s · 20 m/s / 50 m = 8 m/s²). |
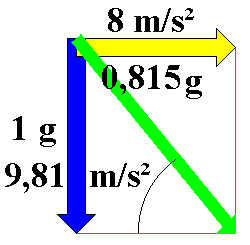
| Zusammensetzung von Kräften in einem Kräfteparallelogramm |
Der blaue Vektor der Erdbeschleunigung von 1 g oder 9,81 m/s² wirkt senkrecht nach unten, der gelbe Vektor der Kurvenbeschleunigung wirkt mit 8 m/s² waagerecht in Richtung der Kurve und entspricht 81,5 % der Erdbeschleunigung (0,815 g). Der grüne Vektor ist die resultierende Beschleunigung, sie beträgt 12,658 m/s². Die Richtung des resultierenden Vektors wird auch als Scheinlot bezeichnet.
 |
Ein Motorradfahrer muss sich - auf die Senkrechte bezogen - um 39,2° in die Kurve legen, um diese Kraft auszugleichen. Mit der Horizontalen bildet sein Motorrad dann einen Winkel von 50,8° (tan α = 9,81 m/s² : 8 m/s² = 1,22625).
Er wird dann mit dem ca. 1,3fachen seiner Normalkraft auf den Boden gedrückt
(12,658 m/s² : 9,81 m/s²).
Werden Beschleunigungen statt in m/s² in Bruchteilen oder Mehrfachen der Erdbeschleunigung (g) angegeben, lassen sich die Kräfte mit hinreichender Genauigkeit sofort in der Einheit Dekanewton (daN) ermitteln, wenn die Masse in Kilogramm (kg) angegeben ist.
Befindet sich eine Masse innerhalb eines beschleunigten Bezugsystems, zeigt der Vektor einer auf eine Masse wirkende Trägheitskraft in die Gegenrichtung zur Beschleunigung. Als Beispiel mag ein Autofahrer dienen, der beim Gasgeben in den Sitz gedrückt wird (positiv gerichtete Beschleunigung und negativ gerichtete Trägheitskraft) bzw. beim Bremsen nach vorn gezogen wird (negativ gerichtete Beschleunigung und positiv gerichtete Trägheitskraft).
Reibungskräfte sind passive Kräfte. Sie werden wirksam, wenn Körper durch Kräfte auf einer Unterlage in Bewegung gesetzt werden sollen (Haftreibung) oder bereits fortbewegt werden (Gleitreibung und Rollreibung). Haftreibung wird auch wirksam, wenn aus einer Bewegung heraus (bei vorliegender Gleit- oder Rollreibung) die Richtung geändert wird. Als Beispiel mag ein Auto bei der Kurvenfahrt dienen. Hier hält nur eine ausreichend große Haftreibung der Reifen das Fahrzeug in der gewünschten Spur (in der Realität sind die Vorgänge komplexer als hier dargestellt). Reibungskräfte wirken den angreifenden Kräften entgegen. Die Größe von Reibungskräften lässt sich mit folgenden Formeln bestimmen.
Die Normalkraft senkrecht zur Gleitfläche kann in N, daN, kN oder ähnlichen Krafteinheiten angegeben werden. Da die jeweiligen Reibungskoeffizienten dimensionslos sind, ergibt sich für die ermittelte Reibungskraft die gleiche Rechendimension wie für die Normalkraft senkrecht zur Gleitfläche.
Da das Thema Reibung für die Ladungssicherung von großer Bedeutung ist, werden einige ausführlichere Anmerkungen in einem gesonderten Abschnitt gegeben.
Schwingungen und Stöße der Fahrzeuge und eingesetzten Geräte sowie Eigen- und Resonanzschwingungen der Güter, Verpackungen und Polstermittel bestimmen überwiegend das Beschädigungsrisiko von Waren während der Beförderung. Von entscheidender Bedeutung ist dabei die Größe der auftretenden Impulse, d. h. die zeitliche Dauer von Kräften bzw. die Geschwindigkeit von Massen.
Hinweis: Zur schadenfreien Verpackung und Beförderung empfindlicher Güter müssen die Frequenzspektren bei Lagerung, Umschlag und Transport sowie die Eigenfrequenzen der Versandgüter, Versandpackungen, Polstermittel usw. bekannt sein. Für den hochfrequenten Bereich haben Messungen außergewöhnlich große Beschleunigungswerte von mehreren Dutzend bis zu einigen Hundert g ergeben. Aufgrund der Massenträgheit der Versandstücke führen diese sehr kurzzeitig wirkenden Stöße jedoch selten zu Schäden infolge mangelhafter Ladungssicherung. Der Versender einer Ware muss diesen Schwingungen bei empfindlichen Gütern jedoch durch entsprechende Verpackungen entgegenwirken. Im niederfrequenten Bereich auftretende Transport- und Umschlagbeschleunigungen bewegen sich im Bereich von g-Bruchteilen bis zu einigen g. Die relativ längere Einwirkzeit kann zu Ladungsverschub und entsprechenden mechanischen Schäden führen. Diese niedrigen "Normalwerte" werden von verschiedenen Organisationen für den Bereich der Ladungssicherung auf oder in Fahrzeugen angegeben. Kenntnis der gängigen g-Werte muss bei Versandbeteiligten vorausgesetzt werden.
Mechanisch-dynamische Beanspruchungen werden in ihren Auswirkungen häufig unterschätzt, obgleich die "normalen Werte" vielerorts zugänglich sind oder leicht erfragt werden können. In den CTU-Richtlinien sind dazu eine Reihe von Anmerkungen gemacht.
Anmerkung: Über die im Abschnitt 1.9 der CTU-Richtlinien wiedergegebenen Tabellen ist zu deren Gestaltung folgendes zu sagen: Die Schreibweise bzw. Formulierungen sind insofern inkorrekt, dass in den Spaltenüberschriften Kräfte genannt werden und in den zugehörigen Feldern die Höhe der Beschleunigungen genannt sind, die derartige Kräfte verursachen. Wenn auf Kräfte abgestellt wird, hätte das "g" als Maß der Erdbeschleunigung von 9,81 m/s² durch "G" als Einheit für die Normalkraft ersetzt werden müssen. Sollen die Tabellenwerte jedoch die Höhe der Beschleunigungen ausdrücken, hätte jeweils das Wort "Kräfte" in den Spaltenüberschriften durch das Wort Beschleunigungen ersetzt werden müssen. Sinngemäßes gilt für die Formulierungen in den Fußnoten zu den Tabellen.