Vibration comprises periodic oscillations which generally occur in large numbers, such as vehicle or engine vibration, movement of ship in rough seas etc.
Jolting comprises occasional events, as may be observed on impact, dropping or tipping. Bumping, kicking or switching impacts are all words which paint a sufficiently clear picture.
The absolute magnitude of both types of stress is measured from their amplitude. For vibration, the second important parameter is frequency, i.e. the number of periodically repeating oscillations within a specific period [cycles/second]. For jolting, pulse duration and frequency are the other determining factors in addition to amplitude.
Dynamic mechanical shipping stresses are accordingly primarily caused by acceleration arising from changes in direction or speed. Acceleration values are particularly high if these changes occur very rapidly. The formulae clarify the relationship:
since
, it follows that linear acceleration may be calculated from the following formula:
If a car accelerates from 0 km/h to 108 km/h in 12 seconds, its speed has changed by 9 km/h or 2.5 m/s each second.
Its acceleration, a, is thus 9 km/h/s or, stated in other terms:
2.5 m/s·s or 2.5 m/s If a truck traveling at a speed of 90 km/h takes five seconds to come to a standstill, it is decelerating at 18 km/h per second or 5 m/s per second. This is precisely the braking deceleration of 5 m/s² specified in the German road traffic licensing regulations (StVZO) and German accident prevention regulations.
A ship which, while pitching in a heavy sea, suffers a loss of speed from 21 knots to 9.3 knots within 2 seconds undergoes negative acceleration of
-11.7 kn/2 s = -5.85 kn/s = -10.834 km/h/s = -3 m/s² and is thus decelerated.
Acceleration arising from a change in direction may be calculated in accordance with the following formula:
If a road vehicle takes a tight curve with a curve radius of 20 m at a speed of 36 km/h, which corresponds to 10 m/s, it undergoes radial acceleration of 5 m/s².
Driving through potholes also causes radial acceleration because there is a change in direction from the horizontal to the vertical and back again. In vehicles with poor shock absorption, this causes considerable acceleration as the curve radii are very small and the speeds at which they are driven through are relatively high. In this case, only the suspension and other design parameters protect the vehicle and its load from severe damage. In roll trailers without suspension, rough ground in the terminal may result in high levels of acceleration and consequent damage to the cargo. It is a relatively frequent occurrence for shipping packages to fall off the trailers during such transport operations within cargo handling facilities.
 |
The action of gravity subjects any object on the earth to downwards acceleration, which is known as acceleration due to gravity. The value of this acceleration is constant. Acceleration due to gravity, rounded to two decimal places, is 9.81 m/s² and is designated 1 g. For rough calculations, 1 g may also be assumed to have a value of 10 m/s². In order to appreciate quite what an acceleration of 1 g means, imagine a road vehicle accelerating from 0 km/h to just about 106 km/h in 3 seconds. The calculation is as follows: |
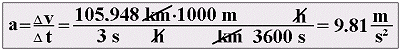
If the magnitude of an acceleration is known, the force it applies to a mass may be calculated from Newton's second law of motion:
The formulae are conventionally written:
On earth, force and weight are physically identical. As a result of acceleration due to gravity, an object of a mass of 100 kg exerts a force of F = 100 kg x 9.81 m/s² = 981 N on whatever is supporting it. Stated in other units, this force amounts to 98.1 daN (decanewtons) or 0.981 kN (kilonewtons).
Weight-force should accordingly be taken to mean the force with which an object is attracted by the earth's gravity. This force always acts perpendicularly downwards. The formula used is as above, but replacing the general abbreviation F for Force with G.
Some publications, such as for example the VDI Guidelines, mention normal force and the abbreviation F is provided with the index N, giving FN = normal force.
Force and acceleration are vector quantities, i.e. quantities in which both magnitude and direction must be stated. Acceleration due to gravity g, however, is always in the same direction as weight.
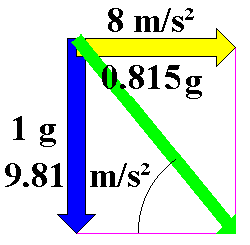 |
A motorcycle rider traveling around a corner with a radius of 50 m at 72 km/h will experience radial acceleration of 8 m/s² (ar= v²/t = 20 m/s x 20 m/s / 50 m = 8 m/s²). |
| Composition of forces in a parallelogram of forces |
The blue vector of acceleration due to gravity of 1 g or 9.81 m/s² acts perpendicularly downwards, the yellow vector of radial acceleration of 8 m/s² acts horizontally in the direction of the curve and corresponds to 81.5% of acceleration due to gravity (0.815 g). The green vector is the resultant acceleration of 12.658 m/s². The direction of the resultant vector is also described as the apparent vertical.
 |
A motorcycle rider must lean into the curve by 39.2°, relative to the vertical, in order to offset this force. His motorcycle will then be at an angle of 50.8° to the horizontal (tan \alpha; = 9.81 m/s² ÷ 8 m/s² = 1.22625) and he will be pressed down towards the ground with approx. 1.3 times his normal force (12.658 m/s² ÷ 9.81 m/s²).
If, instead of being stated in m/s², acceleration values are given in fractions or multiples of acceleration due to gravity (g), the forces may be determined with sufficient accuracy directly in decanewtons (daN), if mass is stated in kilograms (kg).
If the mass is located within a frame of reference under acceleration, the vector exhibits an inertia force acting on the mass in the opposite direction to the acceleration. An example of this is the automobile driver who, on accelerating, is pressed back into his seat (positive acceleration and negative inertia force) or, on braking, is pulled forward (negative acceleration and positive inertia force).
Friction forces are passive forces, which come into play when objects on a substrate are to be set in motion by forces (static friction) or are to be kept in motion (sliding friction and rolling friction). Static friction also comes into play when the direction of motion of an object (already subject to sliding or rolling friction) is changed. An automobile cornering is a good example, as all that keeps the vehicle on its desired path is the sufficient static friction of the tires (in reality, the phenomena at play are more complex than shown here). Friction forces counteract incident forces. The following formulae may be used to calculate the size of friction forces.
The normal force perpendicular to the sliding surface may be stated in N, daN, kN or similar units of force. Since the various coefficients of friction are dimensionless, the determined friction force has the same calculation dimension as for the normal force perpendicular to the sliding surface.
Since friction is of great significance to cargo securing, more detailed explanations will be provided in another section.
Vibration and jolting of the vehicles and equipment used, together with the fundamental and resonant vibration of goods, packaging and cushioning material together largely define the risk of damage to which the goods are exposed during carriage. The magnitude of the pulses, i.e. the duration of forces or velocity of masses, is of vital significance in this connection.
Note: If sensitive goods are to be packaged and carried without suffering damage, it is essential to be aware not only of the frequency spectra which arise during storage, handling and transport but also of the natural frequencies of the goods being shipped, the shipping packages, cushioning material etc. In the high frequency range, extremely high acceleration values of several dozen to a few hundred g have been measured. However, due to the mass inertia of the shipping packages, such short duration impacts rarely cause damage due to inadequate cargo securing. However, the consignor must provide appropriate packaging for sensitive goods in order to mitigate such vibration. In the low frequency range, acceleration values encountered during transport and handling are of the order of some fractions of a g to several g. The longer period of action may result in shifting of the cargo and consequent mechanical damage. These low "normal values" applying to cargo securing on or in vehicles are stated by various organizations. Those involved with shipping should be aware of usual g values.
The effects of dynamic mechanical shipping stresses are frequently underestimated, despite the "normal values" being widely available or easily obtainable. The CTU packing guidelines contain various comments on this issue.
Note: The following comments may be made regarding the tables shown in section 1.9 of the CTU packing guidelines: the wording/notation is incorrect in that forces are stated in the column headings, while the level of acceleration caused by such forces is stated in the associated fields. If forces are the intended meaning, "g" as a measure of acceleration due to gravity of 9.81 m/s² ought to be replaced by "G" as a unit for the normal force. If, however, the values in the table are intended to indicate the level of acceleration, the word "forces" in the column headings ought in each case to be replaced by "acceleration". The same applies to the wording of the footnotes to the tables.